Two satellites \(A\) and \(B\) go around the earth in circular orbits at heights of \(R_A ~\text{and}~R_B\) respectively from the surface of the earth. Assuming earth to be a uniform sphere of radius \(R_e\), the ratio of the magnitudes of their orbital velocities is:
| 1. | \(\sqrt{\frac{R_{B}}{R_{A}}}\) | 2. | \(\frac{R_{B} + R_{e}}{R_{A} + R_{e}}\) |
| 3. | \(\sqrt{\frac{R_{B} + R_{e}}{R_{A} + R_{e}}}\) | 4. | \(\left(\frac{R_{A}}{R_{B}}\right)^{2}\) |
A satellite of mass m is orbiting around the earth at a height h above the surface of the earth is M and its radius is R. The angular momentum of the satellite is independent of
1. m
2. M
3. h
4. none of these
A satellite orbiting around earth of radius R is shifted to an orbit of radius 2R. How many times has the time taken for one revolution increase?
1. 8 times
2. 2 times
3. 2.5 times
4. 2.8 times
If a particle is fired vertically upwards from the surface of earth and reaches a height of 6400 km, the initial velocity of the particle is (Assume R = 6400 km and g = 10)
1. 4 km/sec
2. 2 km/sec
3. 8 km/sec
4. 16 km/sec
A mass M is split into two parts, m and (M-m), which are then separated by a certain distance. What ratio of m/M maximizes the gravitational force between the two parts
1. 1/3
2. 1/2
3. 1/4
4. 1/5
If the radius of the earth were to shrink by 1% its mass remaining the same, the acceleration due to gravity on the earth's surface would
1. Decrease by 2%
2. Remain unchanged
3. Increase by 2%
4. Increase by 1%
Imagine a light planet revolving around a very massive star in a circular orbit of radius R with a period of revolution T. If the gravitational force of attraction between planet and star is proportional to , then is proportional to
1.
2.
3.
4.
A simple pendulum has a time period when on the earth's surface and when taken to a height R above the earth's surface, where R is the radius of the earth. The value of / is
1. 1
2.
3. 4
4. 2
A rocket mass m is launched vertically from the surface of the earth with an initial speed V. Assuming the radius of the earth to be R and negligible air resistance, the maximum height attained by the rocket above the surface of the earth is
1.
2.
3.
4.
A project is project with velocity kv in vertically upward direction from the ground
into the space (V is escape velocity and K<1). If air resistance is considered to be
negligible then the maximum height from the centre of earth to which it can go, will be
: (R=radius of earth)
1.
2.
3.
4.
A satellite is launched into a circular orbit of radius R around the earth. A second
satellite is launched into an orbit of the radius (1.01R) . The period of the second satellite is
larger than that on the first one by approximately
1.0.5%
2.1.0%
3.1.5%
4.3.0%
lf the distance between the earth and the sund becomes hal of its present value, the
number of days in a year would have been
1. 64.5
2. 129
3. 182.5
4. 730
A geostationary satellite orbits around the earth in a circular orbidt of radius 36000
km. Then , the time period of a satellite orbiting a few hundred kilometres above the
earth's surface ( will approximately be
1. 1/2 h
2. 1 h
3. 2 h
4. 4 h
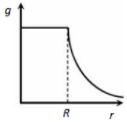
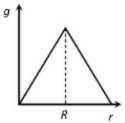
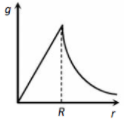
Assuming the earth to have a constant density, point out which of the following curves show the variation of acceleration due to gravity from the centre of earth to the points far away from the surface of earth
1. 
2. 
3. 
4. none of these
A planet of mass m is moving in an elleptical orbit of major axis 2a and miner axis 2b
with angular momentum L. Its period will be
1.
2.
3.
4.
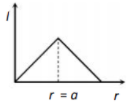
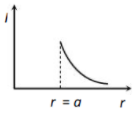
Which one of the following graphs represents correctly the variation of the gravitational field (I) with the distance (r) from the centre of a spherical shell of mass M and radius a
1. 
2. 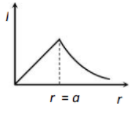
3. 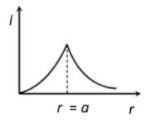
4. 
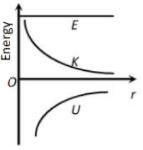
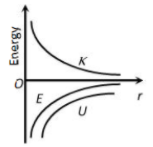
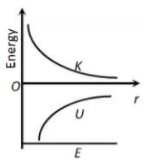
The correct graph representing the variation of total energy (E) kinetic energy (K) and potential energy (U) of a satellite with its distance from the centre of earth is
1. 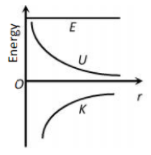
2. 
3. 
4. 
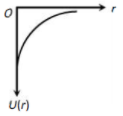
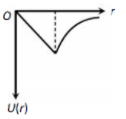
A shell of mass M and radius R has a point mass m placed at a distance r from its center. The gravitational potential energy U (r) vs r will be
1. 
2. 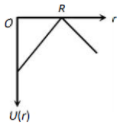
3. 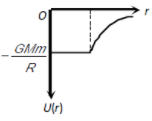
4. 
A body of mass m is taken from earth surface to the height h equal to the radius of the earth, the increase in potential energy will be
1. mgR
2.
3. 2 mgR
4.
An artificial satelite moving in a circular orbit around the earth has toal (Kinetic +
potential) energy E Its potential energy is
1. E
2. 1.5 E
3. 2 E
4. E