A cuboidal block of height a nad width b is placed on the horizontal surface with sufficient friction then for a given force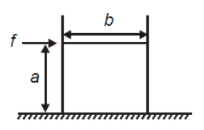
1. Probability of toppling is more of b > a
2. Probability of toppling is more of a > b
3. Probability of toppling is more of a = b
4. Block will not topple
Calculate the velocity of the center of mass of the system of two particles each of mass 2 kg as shown in figure
1. 5 m/s
2. 10 m/s
3. 2.5 m/s
4. 15 m/s
A rod of length 2l is bent as shown in figure. Coordinates of centre of mass are 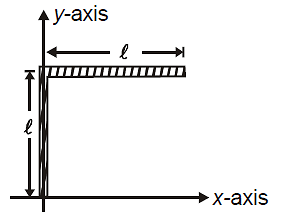
1.
2.
3.
4.
A stick of length L mass M initially upright on a frictionless floor, starts falling, then
1. Center of mass will fall vertically down
2. Centre of mass will follow a circular path
3. Centre of mass will follow any curve path
4. All of these
A disc of radius R and mass M is under pure rolling when a force f is applied at the top most point (as shown in figure) and there is sufficient friction between the disc and the horizontal surface, then 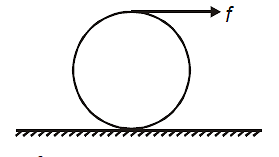
1.
2.
3.
4. None of these
A shell following a parabolic path explodes somewhere in its fight. The centre of mass of fragments will move in
1. Tangential direction
2. Radial direction
3. Horizontal direction
4. Same parabolic path
A ring of mass m and radius R is acted upon by a force F as shown in the figure, there is sufficient friction between the ring and the ground then the force of friction necessary for pure rolling is 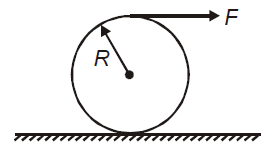
1. forward
2. forward
3. Zero
4. backward
An elliptical disc shown in the figure is rotated turn about x-x', y-y' and z-z' axes passing through the centre of mass of the disc. Moment of inertia of the disc is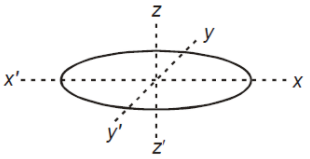
1. Same about all the three axes
2. Maximum about z-z' axes
3. Maximum about y-y' axis
4. Same about x-x' and y-y' axis
A particle of mass m = 3 kg is projected at an angle of with the horizontal with a speed of m/s. The angular momentum of the particle at the highest point of trajectory about a horizontal axis passing through the origin and perpendicular to the plane of motion is
1. 1200 Js
2. 1600 Js
3. 1500 Js
4. 2000 Js
Moment of inertia of a rod of mass m and length/ about an axis at a distance from oneof the ends of the rod and perpendicular to its length is
1.
2.
3.
4.
A rod of length L is hinged at one end. It is brought to a horizontal position and released. The angular velocity of the rod when it is in a vertical position is
1.
2.
3.
4.
If a spherical ball is under pure rolling on a table, then the fraction of its total kinetic energy associated with rotation is
1.
2.
3.
4.
An automobile engine develops W power when rotating at a speed of 1800 rad/minute. The average torque delivered by the engine is
1. Nm
2. Nm
3. Nm
4. Nm
A wheel starts from rest na attains an angular velocity of 20 rev/s after being uniformly accelerated for 20 s . The total angle is radian through which it has turned in 10 s is
1. 200
2. 40
3. 150
4. 100
A solid cylinder, a solid sphere, and a hollow sphere each of mass m and radius r are released from the top of a smooth inclined plane. Then which of the bodies has minimum acceleration down the plane?
1. Solid cylinder
2. Solid sphere
3. Hollow sphere
4. All have same acceleration
A solid cylinder of mass m and radius r is rolling with angular speed on a horizontal plane. The magnitude of its angular momentum about origin O is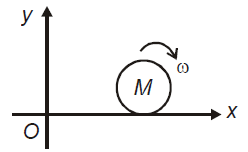
1.
2. 1.5
3. 2
4. 2.5
Choose the incorrect statement
1. The centre of mass of a two-particle system lies on the line joining the two particles, being closer to the heavier particle
2. In rolling, the point of contact of the rolling body remains at rest relative to the surface on which it is rolling
3. Parallel axis theorem is applicable only for laminar bodies
4. A particle moving on a straight line may have non-zero angular momentum about a point
John is standing with folded hands at the centre of a platform rotating about its central axis. The kinetic energy of the system is K. Now, John stretches his arms so that moment of inertia of the system doubles. The kinetic energy of the system now is
1. 2K
2. 4K
3. K/4
4. K/2
A solid cylinder of mass m and radius r is rotating about its longitudinal axis (vertical with an angular speed . If a disc of mass 2m and radius 2r is gently placed on it coaxially, then the new angular velocity of the system is
1.
2.
3.
4.
Calculate the torque acting on the disc in the given arrangement (Radius of disc 1m and mass m)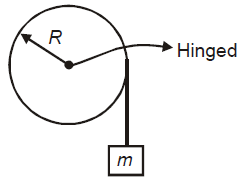
1. 2 mg/3
2. mg/3
3. mg
4. 4 mg/s
The speed of the centre of mass of a homogenous sphere after rolling down an inclined plane of vertical height h from rest without sliding is
1.
2.
3.
4.
A rod of mass 4m and length l hinged at its centre is placed on a horizontal surface. A bullet of mass m moving with velocity v strikes the end A of the rod and gets embedded in it. The angular velocity with which the system rotates about its centre of mass after the bullet strikes the rod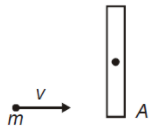
1.
2.
3.
4.
The magnitude of the angular momentum of a wheel change from 2L to 3L in 5 sec. by a constant torque acting opposite to the initial direction of rotation. What is the magnitude of the torque?
1.
2. L
3.
4.
A solid cylinder is rolling without slipping with a velocity of its centre of mass v and angular velocity of its centre of mass on a horizontal frictionless surface as shown in the figure. If it collides with a frictionless vertical wall X, then after collision its velocity and angular velocity respectively become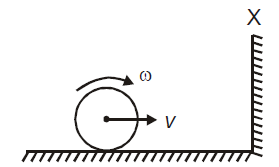
1.
2.
3.
4.