The mass of a body measured by a physical balance in a lift at rest is found to be m. If the lift is going up with an acceleration a, its mass will be measured as
1.
2.
3. m
4. Zero
When forces are acting on a particle of mass such that are mutually perpendicular, then the particle remains stationary. If the force is now removed then the acceleration of the particle is:
1. \(\mathrm{F_1}/\mathrm{m}\)
2. \(\mathrm{F_2}\mathrm{F_3}/\mathrm{m}\mathrm{F_1}\)
3. \(\mathrm{F_2}-\mathrm{F_3}/\mathrm{m}\)
4. \(\mathrm{F_2}/\mathrm{m}\)
A string of negligible mass going over a clamped pulley of mass m supports a block of mass M as shown in the figure. The force on the pulley by the clamp is given by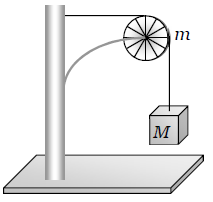
1.
2.
3.
4.
A solid sphere of mass \(2\) kg is resting inside a cube as shown in the figure. The cube is moving a velocity \(v=(5t\hat{i}+2t \hat{j})\) m/s. Here \(t\) is the time in second. All surface are smooth. The sphere is at rest with respect to the cube. What is the total force exerted by the sphere on the cube?
(Take \(g=10\) m/s2 )
1. \(\sqrt{29}\) N
2. \(29\) N
3. \(26\) N
4. \(\sqrt{89}\) N
A flat moves normally with a speed v towards horizontal jet of water of uniform area of cross-section. The jet discharges water at the rate of volume V per second at a speed v .The density of water p. Assume that water splashes along the surface of the plate at right angles to the original motion. The magnitude of the forces acting on the plate due to the jet of water is
1.
2.
3.
4.
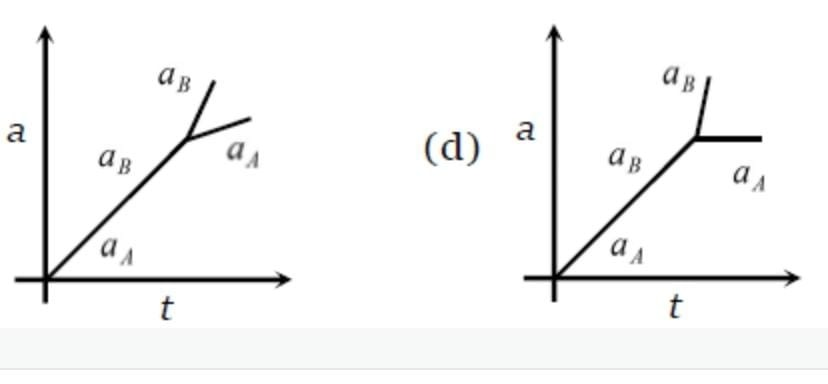
A block B is placed on block A. The mass of block B is less than the mass of block A,
Friction exists between the blocks, whereas the ground on which the block A is placed
is taken to be smooth. A horizontal force F, increasing linearly with time begins to act
on B. The acceleration a and a of blocks A and B respectively are plotted against t.
The correctly plotted graph is 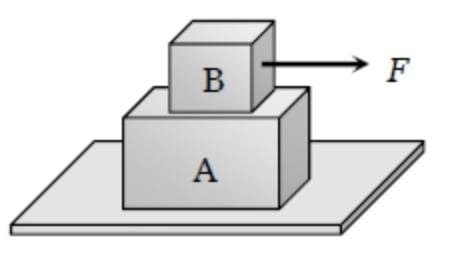
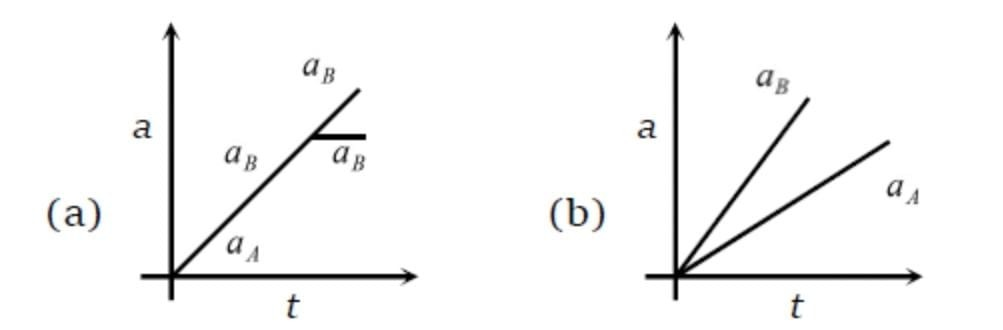
In the figure given below, the position-time graph of a particle of mass \(0.1\) kg is shown. The impulse at \(t=2\) s is:

1. \(0.2\) kg ms-1
2. \(-0.2\) kg ms-1
3. \(0.1\) kg ms-1
4. \(-0.4\) kg ms-1
The force-time (F - t) curve of a particle executing linear motion is as shown in the figure. The momentum acquired by the particle in time interval from zero to 8 second will be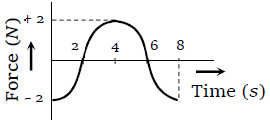
1. -2 N-s
2. +4 N-s
3. 6 N-s
4. Zero
A particle of mass \(m,\) initially at rest, is acted upon by a variable force, \(F\) for a brief interval of time \(T.\) It begins to move with a velocity \(u\) after the force stops acting \(F\) is shown in the graph as a function of time. The curve is a semicircle. Then:

| 1. | \(u=\dfrac{\pi F^{2}_{0}}{2m}\) | 2. | \(u=\dfrac{\pi T^{2}_{}}{8m}\) |
| 3. | \(u=\dfrac{\pi F^{}_{0}T}{4m}\) | 4. | \(u=\dfrac{ F^{}_{0}T}{2m}\) |
A uniform chain of length L changes partly from a table which is kept in equilibrium by
friction. The maximum length that can withstand without slipping is l, then coefficient
of friction between the table and the chain is
1.
2.
3.
4.
A horizontal force of \(10~\text{N}\) is necessary to just hold a block and the wall is \(0.2\). The weight of the block is:

1. \(2~\text{N}\)
2. \(20~\text{N}\)
3. \(50~\text{N}\)
4. \(100~\text{N}\)
A given object takes n times as much time to slide down a 45 rough incline as it takes
to slide down a perfectly smooth 45 incline. The coeficient of kinetic freiction between
the object and th incline is given by
1.
2.
3.
4.
The maximum speed that can be achieved without skidding by a car on a circular unbanked road of radius R and coeffiecient of static friction , is
1. Rg
2.
3.
4.
Two carts of masses 200 kg and 300 kg on horizontal rails are pushed apart. Suppose the coefficient of friction between the carts and the rails are same. If the 200 kg cart travels a distance of 36 m and stops, then the distance travelled by the cart weighing 300 kg is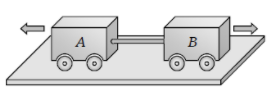
1. 32 m
2. 24 m
3. 16 m
4. 12 m
A vehicle of mass m is moving on a rough horizontal road with momentum P, If the coefficient of friction between the tyres and the road be , then the stopping distance is
1.
2.
3.
4.
A block of mass m lying on a rough horizontal plane is acted upon by a horizontal force
P and another force Q inclined at an angle to the verticlal. The block will remain in
equilibrium, if the coefficient of friction between it and the surface is
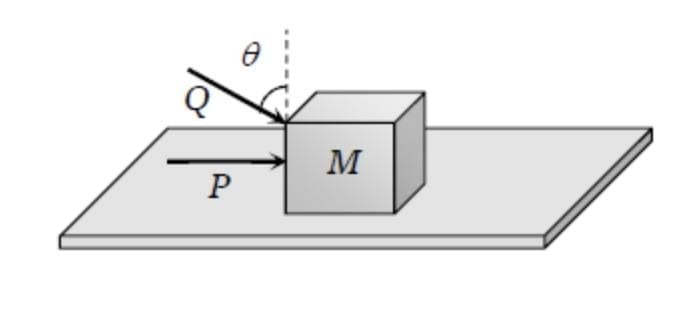
1.
2.
3.
4.
A body of mass \(M\) is kept on a rough horizontal surface (friction coefficient \(\mu)\). A person is trying to pull the body by applying a horizontal force but the body is not moving. The force by the surface on the body is \(F\), where:
1. \(F = Mg\)
2. \(F = \mu Mg\)
3. \(Mg \leq F\leq Mg \sqrt{1+\mu^2}\)
4. \(Mg \geq F\geq Mg \sqrt{1+\mu^2}\)
What is the maximum value of the force F such that the block shown in the arrangement, does not move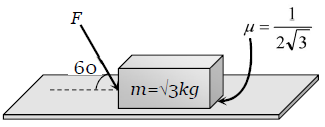
1. 20 N
2. 10 N
3. 12 N
4. 15 N
A 40 kg slab rests on a frictionless floor as shown in the figure. A 10 kg block rests on the slab. The static coefficient of friction between the block and slab is 0.60 while the kinetic freiction is 0.40. The 10 kg block is kinetic friction is 0.40. The 10 kg block is acted upon by a horizontal force 100 N. If g=9.8 m/s , the resulting acceleration of the slab will be
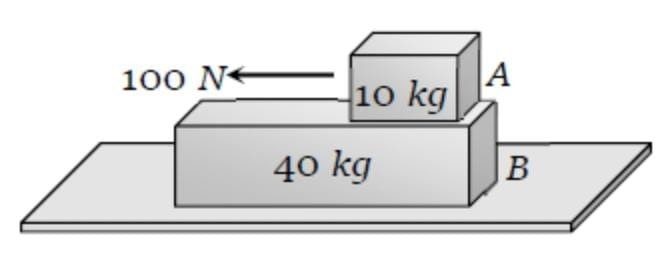
1. 0.98 m/s
2. 1.47 m/s
3. 1.52 m/s
4. 6.1m/s
A block of mass 2 Kg rests on a rough inclined place making an angle of 30 with the
horizontal. The coefficient of static friction between the block and the plane is 0.7. the frictional force on the block is
1. 9.8 N
2. 0.7
3.
4. 0.8