The radii of two circles are 13 cm and 6 cm. respectively. Find the radius of the circles which has the circumference equal to the sum of the circumferences of the two circles.
The cost of fencing a circular field at the rate of ₹ 24 per meter is ₹ 5280. The field is to be ploughed at the rate of ₹ 0.50 per Find the cost of ploughing the field.
The circular footpath of width 2 m is constructed at the rate of ₹ 20 per around a circular park of radius 1500 m. Find the total cost of construction of the footpath.
If the area of a semi-circular field is 30800 sq. m, then find the perimeter of the field.
the radius of the wheel of a bus is 25 cm. If the speed of the bus is 33 km/h, then how many revolutions will the wheel make in 1 min?
the short and long hands of a clock are 6 cm and 8 cm long respectively, find the sum of the distance travelled by their tips in 1 day.
The shaded area in the adjacent figure between the circumference of two concentric circles is The circumference of the inner circle is 88 cm. calculate the radius of the outer circle.
the ratio of the outer and inner circumference of a circular path is 23:22. If the path is 5 m wide, then find the diameter of the inner circle.
Two circles touch each other externally. The sum of their areas is 130 and the distance between their centers is 14 cm. Find the radii of the circles.
A boy is cycling such that the wheels of the cycle are making 140 revolutions per minute. If the diameter of the wheel is 60 cm, then find the speed per hour with which the boy is cycling.
If the perimeter of a circle is equal to that of a square, then find the ratio of their areas.
Two parallel lines touch the circle at points A and B, respectively. If the area of the circle is 25, then find the length of AB.
A wire when bent in the form of a square enclose an area 121 sq cm. If the wire was bent in the form of a circle, then find the area enclosed by the circle.
the length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in one minute.
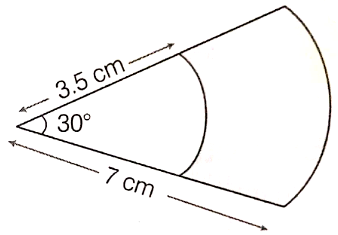
In a circle of radius 28 cm, an arc subtends an angle of at the center. Find the length of the arc and using it, find the area of the sector.
the length of an hour hand of a clock is 7 cm. Find the area swept by the hour hand in one hour.
The minute hand of a clock is 12 cm long. Find the area of the face of the clock described by the minute hand between 9 am and 9:35 cm.
In a circle of radius 21 cm, an arc subtends an angle of at the center. Find the length of the arc.
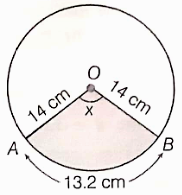
In the given figure. O is the center of the circle with a radius equal to 14 cm. The length of the arc AB = 13.2 cm. Find the area of the shaded sector of the circle.
Area of a sector of a circle of radius 36 cm is 54 Find the length of the corresponding arc of the sector.
A cow is tied with a rope of length 14 m at the corner of a rectangular field of dimensions 20 m x 16 m. Find the area of the field in which the cow can graze.
find the area of the shaded region in the figure as shown below where ABCD is a square of sides 12 cm.
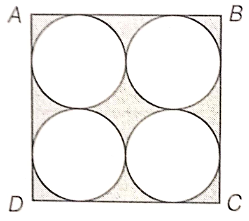
Find the area of shaded design in the given figure, where ABCD is a square of side 10 cm and semi-circles are drawn with each of the sides as diameter.
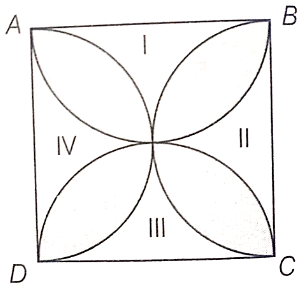
In the given figure, sectors of two concentric circles of radii 7 cm and 3.5 cm are shown. Find the area of the shaded region.
A memento is made as shown in the figure. Its base PBCR is silver plated from the front side at the rate of ₹ 20 per . Find the total cost of the silver plating.
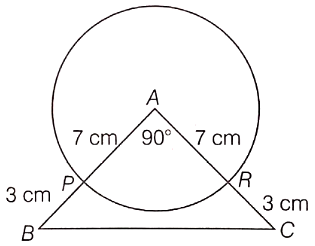
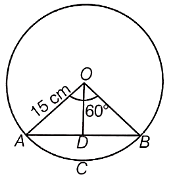
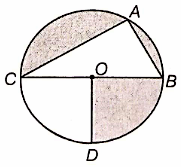
Find the area of the shaded region in the figure, if AC = 20 cm, AB = 15 cm and O is the center of the circle.
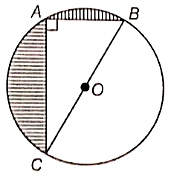
In the adjoining figure, OACBO represents a quadrant of a circle of radius 4.5 cm with center O. Calculate the area of the shaded portion.
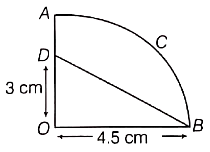
A paper is in the form of a rectangle ABCD in which AB = 20 cm and BC = 14 cm. A semi-circular portion with BC as the diameter is cut-off. Find the area of the remaining part.
From each of the two opposite corners of a square of side 8 cm, a quadrant of a circle of radius 1.4 cm is cut. Another circle of radius 4.2 cm is also cut from the center as shown in the figure. Find the area of the remaining (shaded) portion of the square.
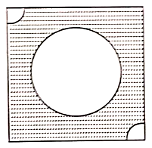
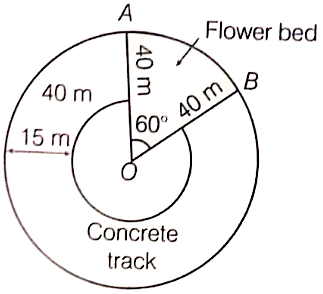
a square park has a side of 100 m. At each corner of the park, there is a flower bed in the form of a quadrant of radius 14 m as shown in the figure below. find the area of the remaining part of the park.
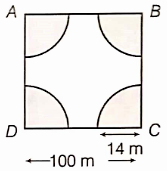
In the given figure, ABCD is a square of side 7 cm and A, B, C, and D are the center of equal circles touching externally in pairs. Find the area of the shaded region.
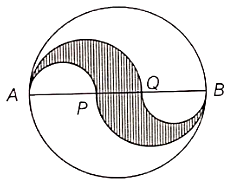
In the given figure, the diameter AB is 12 cm long. AB is trisected at points P and Q. Find the area of the shaded region.
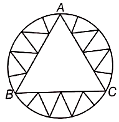
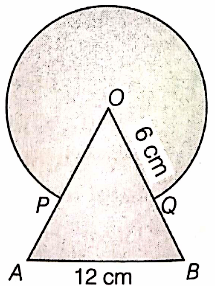
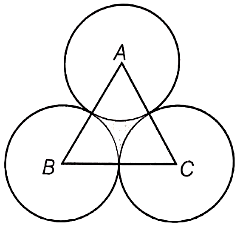
On a circular table cover of radius 42 cm. a design is formed by a girl leaving an equilateral AABC in the middle as shown in the figure. It was decided that the payment to the girl be made proportional to the covered area cf the design. Find the covered area of the design.
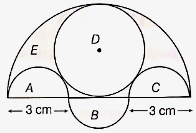
There are three semi-circles A, B, and C having diameter 3 cm each and another semi-circle E having a circle D with diameter 45 cm as shown in the figure below. Find the area of the shaded region.
In the given, PQRS is a rectangle of length and breadth cm. If PEO is an isosceles triangle inscribed in the semi-circle with diameter PQ, then find the area of the shaded region.
The radii of two circles are 8 cm and 6 cm, respectively. Find the radius of the circle having an area equal to the sum of the areas of the two circles.
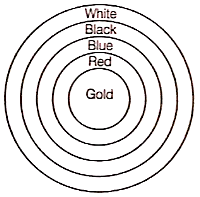
The given figure depicts an archery target marked with its five scoring regions from the centre outwards as gold, red, blue, black and white. The diameter of the region representing the Gold score is 21 cm and each of the other bands is 10.5 cm vide. Find the area of each of the five scoring regions.
The wheels of a car are of diameter 80 cm each. How many complete revolutions does each wheel make in 10 min when the car is traveling at a speed of 66 km per h?
Tick the correct answer in the following and justify your choice. If the perimeter and the area of a circle are numerically equal, then the radius of the circle is
1. 2 units
2. units
3. 4 units
4. 7 units
Find the area of a sector of a circle with radius 6 cm, if angle of the sector is
Find the area of a quadrant of a circle whose circumference is 22 cm.
A chord of a circle of radius 10 cm subtends a right angle at the center. Find the area of the corresponding
(i) minor segment.
(ii) major sector.
In a circle of radius 21 cm, an arc subtends an angle of at the center. Find
(i) The length of the arc
(ii) Area of the segment formed by the arc.
(iii) Area of the segment formed by the corresponding chord.
A chord of a circle of radius 15 cm subtends an angle of at the center. Find the areas of the corresponding minor and major segments of the circle.
A horse is tied to a peg at one corner of a square-shaped grass field of side 15 m by means of a 5 m long rope (see the figure). Find
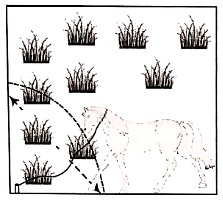
(i) The area of the part of the field in which the horse can graze.
(ii) The increase in the grazing area if the rope was 10m long instead of 5m.
A brooch is made with silver wire in the form of a circle with a diameter of 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in the figure. Find
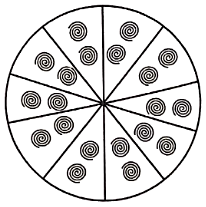
(i) the total length of the silver wire required.
(ii) the area of each sector of the brooch.
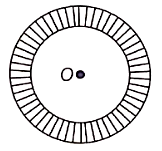
An umbrella has g ribs that are equally spaced (see the figure). Assuming umbrella to be a flat circle of radius '15 cm, find the between the two consecutive ribs of the umbrella.
A car has two wipers that do not overlap. Each wiper has a blade of length 25 cm sweeping Through an angle of Find the total area cleaned at each sweep of the blades.
To warn ships for underwater rocks, a lighthouse spreads a red-colored light over a sector of an angle of to a distance of 16.5 km. Find the area of the sea over which the ships are warned.
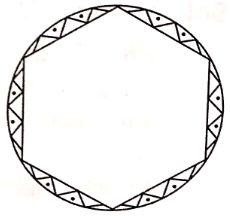
A round table cover has six equal design as shown in the figure. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of ₹ 0.35 per
Find the area of the shaded region in the given figure, if PQ = 24 cm, PR = 7 cm, and O is the center of the circle.
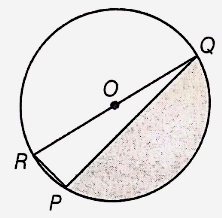
Find the area of the shaded region in the figure, if radii of the two concentric circles with center O are 7 cm and 14 cm respectively and
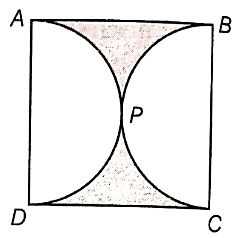
Find the area of the shaded region in the figure, if ABCD is a square of side 14 cm and APD and BPC are semi-circles.
Find the area of the shaded region in the figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of sides 12 cm as the center.
From each corner of a square of side 4 cm, a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in figure. Find the area of the remaining portion of the square.
In a circular table cover of radius 32 cm, a design is formed leaving an equilateral ABC in the middle as shown in the figure. Find the area of the design.
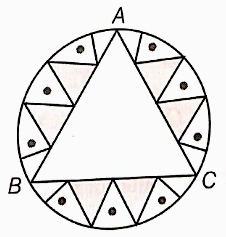
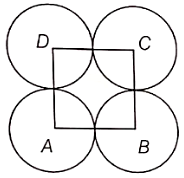
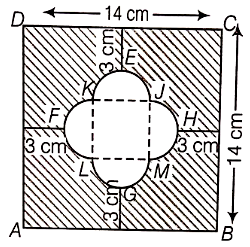
In the adjoining figure, ABCD is a square of side 14 cm, with centers A, B, C, and D, four circles are drawn such that each circle touch externally two of the remaining three circles. Find the area of the shaded region.
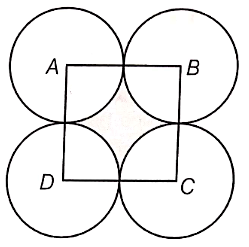
The following figure depicts a racing track whose left and right ends are semi-circular. The distance between two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find
(i) the distance around the track along its inner edge.
(ii) the area of the track.
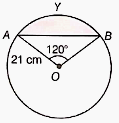
In the given, AB and CD are two diameters of a circle (with the center O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, then find the area of the shaded region.
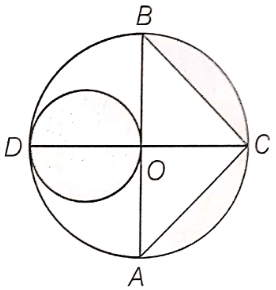
the area of an equilateral ABC is 17320.5 . with each vertex of the triangle as the center, a circle is drawn with a radius equal to half the length of the side of the triangle (see the figure). Find the area of the shaded region.
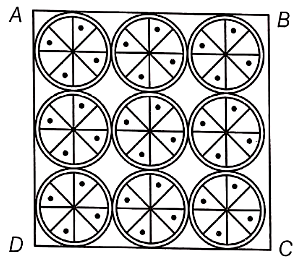
On a square handkerchief, nine circular designs each of radius 7 cm are made (see the figure). Find the area of the remaining portion of the handkerchief.
In the given figure, OACB is a quadrant of a circle with center O and radius 3.5 cm. If OD = 2 cm, then find the area of the shaded region.
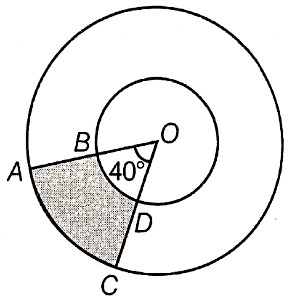
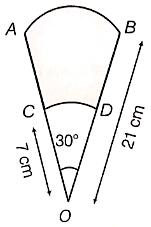
AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and center O (see the figure). If then find the area of the shaded region.
In the given figure, ABC is a quadrant of a circle of radius 14 cm and a semi-circle is drawn with BC as diameter. Find the area of the shaded region.
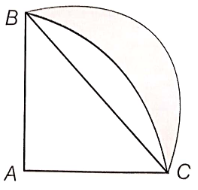
Calculate the area of the designed region in the figure, common between the two quadrants of the circles of radius 8 cm each.
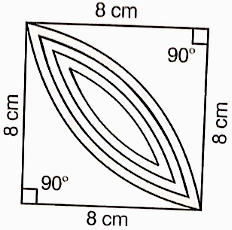
What will be the length of an arc of a sector of a circle with radius r and angle
If the ratio of the circumference of two circles is 3:2, then find the ratio of their areas.
Find the area of the sector of a circle of radius 28 cm and central angle
what will be the perimeter of a quadrant of a circle of radius r?
If the area and circumference of a circle are numerically equal, then find the diameter of the circle.
The sum of the circumference and the radius of a circle is 51 cm. Find the radius of the circle.
The outer and inner diameters of a circular ring are 34 cm and 32 cm respectively, then find the area of the ring.
A garden roller has a circumference of 4 m. Find the number of revolution, it makes in moving 40 m.
If the perimeter of a semi-circular protractor is 36 cm, then find its diameter.
If the area of a sector of a circle is th of the area of that circle, then find the central angle of the sector.
Find the area of a square inscribed in a circle of radius 8 cm.
Find the radius of a circle whose circumference is equal to the sum of the circumference of two circles of radii 15 cm and 18 cm.
The difference between circumference and diameter of a circle is 135 m. Find the radius of the circle.
The circumference of a circle exceeds the diameter by 16.8 cm. Find the radius of the circle.
If the area of a circle is equal to the sum of the areas of two circles of a diameter of the larger circle.
An athlete runs on a circular track of radius 49 m and covers a distance of 3080 m along its boundary. How many rounds has he taken to cover this distance?
Find the perimeter of the given figure, where AED is a semi-circle and ABCD is a rectangle.
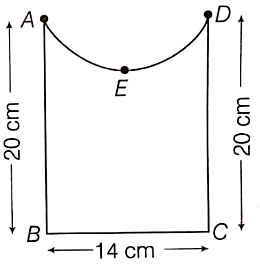
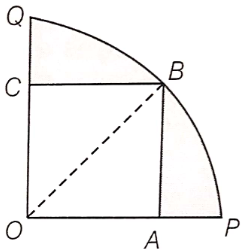
In the given figure, a square is inscribed in a circle of diameter d and another square is circumscribing the circle. Is the area of the outer square four times the area of the inner square? Give a reason for your answer.
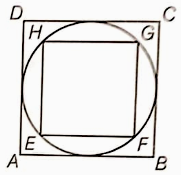
In the figure, a square of diagonal 8 cm is inscribed in a circle. Find the area of the shaded region.
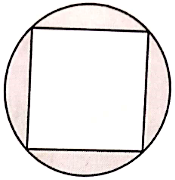
The difference between the circumference and the radius of a circle is 74 cm. Find the area of the circle.
The area enclosed between the concentric circles is 770 If the radius of the outer circle is 21 cm, then find the radius of the inner circle.
The short and long hands of a clock are 4 cm and 6 cm long respectively. Find the sum of distances travelled by their tips in 2 days.
Find the area of the sector of a circle of radius 5 cm, if the corresponding arc length is 3.5 cm.
Find the area of the largest circle that can be drawn inside the given rectangle of length 'a' cm and breadth 'W cm(a > b).
If the length of an arc of a circle of radius r is equal to that of an arc of a circle of radius 2r, then the angle of the corresponding sector of the first circle is double the angle of the corresponding sector of the Other circle. Is this statement false? Why?
In the given figure, arcs are drawn by taking vertices A B and C of an equilateral triangle of side 10 cm, to intersect the sides BC, CA and AB at their respective mid. points D, E and F. Find the area of the shaded region.
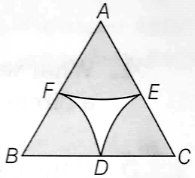
In the given figure, OABC is a square of side 7 cm. If OAPC is a quadrant Of a circle With centre O, then find the area of the shaded region.
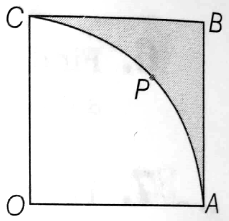
An arc of a circle is oi length cm and the sector it bounds has an area of . Find the radius of the circle.
In the figure given alongside, a circle is inscribed in a square of side 4 cm and another circle is circumscribing the square. Prove that the area of the circumscribed circle is the time the area of the inscribed circle.
In the given figure, find the area of the shaded region.
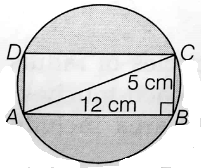
Find the area of the shaded region in the given figure, if BC = BD = 8 cm, AC = AD = 15 cm and O is the center of the circle.
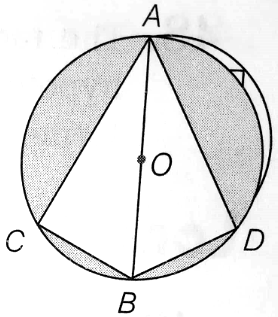
The given figure consists of four small semi-circles of equal radii and two big semi-circles of equal radii (each 42 cm). Find the area and perimeter of the shaded region.
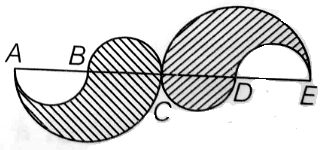
find the area of the shaded portion from the given figure.
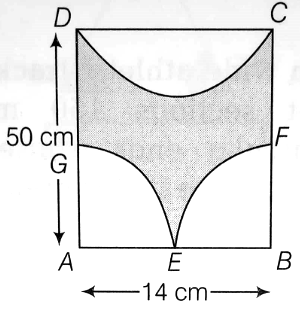
In the given figure, find the area of the shaded portion with given measurement.
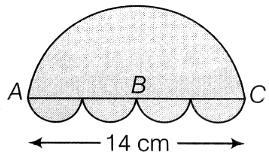
A tool is prepared out of a circular metallic disc of radius 14 cm, by taking out two semi-circular parts of radius 7 cm each from the two sides as shown in the figure. Find the area of the metal used in making 50 such tools.
The radius of the circumcircle of a right-angled triangle is 3 cm and the altitude drawn to the hypotenuse is 2 cm long. Find the sum of the areas of the three disjoint segments of the formed by the sides of this triangle.
Find the area of the shaded region of the given figure.
Sides of a triangular field are 15 m, 16 m, and 17 m. With the three corners of the field a cow, a buffalo, and a horse are tied separately with ropes of length 7 m each to graze in the field. Find the area of the field which cannot be grazed by the three animals.
Find the difference between the areas of a sector of angle and it's a corresponding major sector of a circle of radius 21 cm.
The central angles of two sectors of circles of radii 7 cm and 21 cm are respectively Find the area of the two sectors as well as the lengths of the corresponding arcs. What do you observe?
If three circles of radius each, are drawn such that each touches the other two, then prove that area included between them is equal to
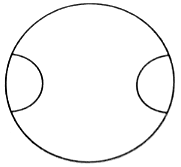
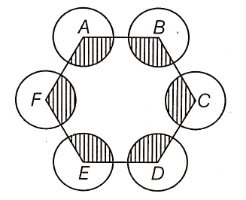
ABCDEF is a regular hexagon. With vertices A, B, C, D, E and F as the centres, circles of the same radius r are drawn. Find the area of the shaded portion shown in the given figure.
For the inauguration of eco-club to the school, badges were given to teachers. Sangeeta made these badges in the shape of an equilateral triangle of side 5 cm with a circle of radius cm inscribed in it as shown in the figure.
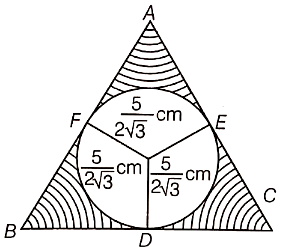
(i) Find the area Of the shaded portion.
(ii) Which value is depicted by Sangeeta?
Two farmers have circular plots. The plots are watered with the same water source placed in the point common to both the plots as shown in the figure. The sum of their areas is 130 and the distance between their centres is 14 m. Find the radii of the circles. What value is depicted by the farmers?
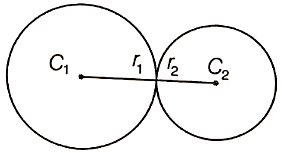
A farmer has a field in the form of a circle. He wants to fence the field. The field is to be ploughed at the rate of ₹ 0.75 per If the cost of fencing of a circular field at the rate of ₹ 25 per m is ₹ 5500, then
(i) find the length of fencing the circular field.
(ii) find the cost of ploughing the field.
(iii) Which value is depicted by the farmer in fencing the field?
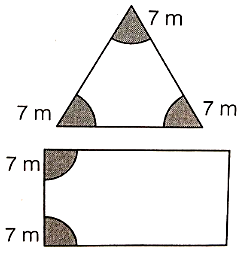
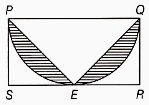
A farmer has two types of fields—in the form of a triangle and a rectangle. Rani is allowed to cut grass in the triangular part (shaded) and Ramu of the rectangular field (shaded). Calculate the areas of the shaded portion. What value is depicted by the farmer?