In the following figure, ΔABC is right-angled at C, and M is the mid-point of hypotenuse AB. If AC = 32 cm and BC = 60 cm, then find the length of .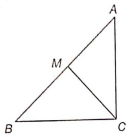
(1) 32 cm
(2) 30 cm
(3) 17 cm
(4) 34 cm
A cyclic polygon has n sides such that each of its interior angle measures 144°. What is the measure of the angle subtended by each of its side at the geometrical centre of the polygon?
(1) 144°
(2) 30°
(3) 36°
(4) 54°
In the following, PQRS is a rhombus. SQ and PR are the diagonals of the rhombus intersecting at O. If angle OPQ = 35°, then find the value of angle ORS + angle OQP.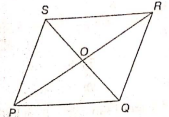
(1) 90°
(2) 180°
(3) 135°
(4) 45°
In the following, CDEF is a cyclic quadrilateral. and are the angle bisectors of ∠C and ∠D respectively. If ∠E = 100° and ∠F = 110°, then find ∠CPD.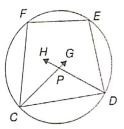
(1) 105°
(2) 80°
(3) 150°
(4) 90°
In the following figure, ABC is an equilateral triangle. DE is parallel to BC and equal to half the length of BC. If AD + EC + CB = 24 cm, then what is the perimeter of triangle ADE?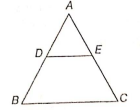
(1) 12 cm
(2) 16 cm
(3) 18 cm
(4) Cannot be determined
In ΔPQR, M and N are points on PQ and PR, respectively, such that . If PM = x, PR = x + 9, PQ = x + 13 and PN = x – 2, then find x.
(1) 10
(2) 11
(3) 13
(4) 15
In the following figure (not to scale), the chords AC and BD intersect at E and ∠BAE = ∠ECD + 20°. If ∠CDE = 60°, find ∠ABE.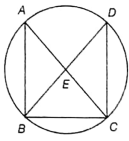
(1) 40°
(2) 60°
(3) 80°
(4) None of these
In the following figure, and are equal chords of the circle subtending ∠DHE and ∠FHG at the point H on the circle. If ∠DHE = , then find ∠FHG.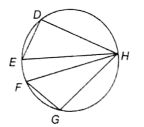
(1)
(2) 30°
(3)
(4) 60°
The bisectors of two adjacent angles in a parallelogram meet at a point P inside the parallelogram. The angle made by these bisectors at a point is _______.
(1) 180°
(2) 90°
(3) 45°
(4) None of these
If x° is the measure of an angle which is equal to its complement and y is the measure of an angle which is equal to its supplement, then is _______.
(1) 1
(2) 3
(3) 0.5
(4) 2
In the following figure, O is the centre of the circle. If ∠MPN = 55°, then find the value of ∠MON + ∠OMN + ∠MNO.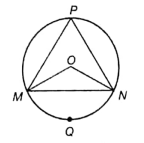
(1) 145°
(2)
(3)
(4) 180°
In the following figure, ΔPQR is right-angled at R and S is the mid-point of hypotenuse PQ. If RS = 25 cm and PR = 48 cm, then find QR.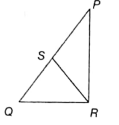
(1) 7 cm
(2) 25 cm
(3) 14 cm
(4) Cannot be determined
In a cyclic quadrilateral PQRS, PS = PQ, RS = RQ and ∠PSQ = 2∠QSR. Find ∠QSR.
(1) 20°
(2) 30°
(3) 40°
(4) 50°
In the following figure, two isosceles right triangles, DEF and HGI are on the same base and is parallel to . If DE = GH = 9 cm and DH = 20 cm, then the area of the quadrilateral FEGI is _______.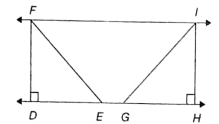
(1) 99 cm2
(2) 40.5 cm2
(3) 81 cm2
(4) 180 cm2
A pole of height 14 m casts a 10 m long shadow on the ground. At the same time, a tower casts a 70 m long shadow on the ground. Find the height of the tower.
(1) 50 m
(2) 78 m
(3) 90 m
(4) 98 m
The angle subtended by a minor arc in its alternate segment is _______.
(1) acute
(2) obtuse
(3) 90°
(4) reflex angle
The number of diagonals of a regular polygon is 27. Then, each of the interior angles of the polygon is _______.
(1)
(2) 140°
(3) 128°
(4) 154°
ABC is a triangle inscribed in a circle, AC being the diameter of the circle. The length of AC is as much more than the length of BC as the length of BC is more than the length of AB. Find AC : AB.
(1) 5 : 3
(2) 5 : 4
(3) 6 : 5
(4) 3 : 2
is the arc of the circle with centre O. If ∠MOR = 100° and ∠NOR = 135°, then ∠ORN + ∠ORM is _______.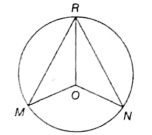
(1)
(2) 40°
(3) 125°
(4)
In the following figure (not to scale), ∠BCD = 40°, ∠EDC = 35°. ∠CBF = 30° and ∠DEG = 40°. Find ∠BAE.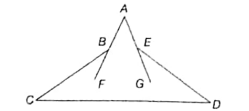
(1) 70°
(2) 50°
(3) 110°
(4) 35°
In the following figure (not to scale), . If ∠BAE = 25° and ∠DCE = 30°, then find ∠AEC.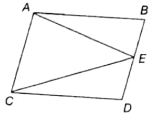
(1) 30°
(2) 45°
(3) 50°
(4) 35°
A tower of height 60 m casts a 40 m long shadow on the ground. At the same time, a needle of height 12 cm casts a x cm long shadow the ground. Find x.
(1) 6
(2) 8
(3) 10
(4) 14
In the given figure, AC is the diameter. AB and AD are equal chords. If ∠AED = 110°, then find ∠BAD.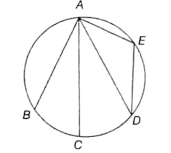
(1) 40°
(2) 55°
(3) 110°
(4) 120°
In the given rectangle ABCD, the sum of the lengths of two diagonals is equal to 52 cm and E is a point in AB, such that is perpendicular to . Find the lengths of the sides of the rectangle, if OE = 5 cm.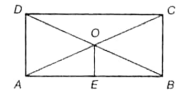
(1) 24 cm, 10 cm
(2) 12 cm, 10 cm
(3) 24 cm, 5 cm
(4) 12 cm, 15 cm
In the following figure (not to scale), AD bisects ∠BAC. If ∠BAD = 45° and ΔABC is inscribed in a circle, then which of the following is the longest?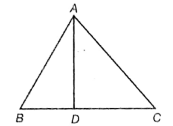
(1) AB
(2) AD
(3) AC
(4) BC
In the given figure, and area of the parallelogram ABFD is 24 cm2. Find the areas of ΔAFB, ΔAGB and ΔAEB.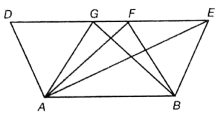
(1) 8 cm2
(2) 12 cm2
(3) 10 cm2
(4) 14 cm2
In the given figure, and intersect at C, such that BC = CE, ∠ABC = 40° and ∠DEC = 85°. Find ∠BAC – ∠CDE.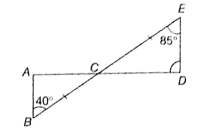
(1) 45°
(2) 125°
(3) 55°
(4) 110°
In the given figure, DEF is a triangle. If DF is the longest side and EF is the shortest side, then which of the following is true?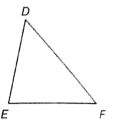
(1) ∠E > ∠D > ∠F
(2) ∠D < ∠F < ∠E
(3) ∠D < ∠E < ∠F
(4) None of these
The ratio between the exterior angle and the interior angle of a regular polygon is 1 : 3. Find the number of the sides of the polygon.
(1) 12
(2) 6
(3) 8
(4) 10
Find each interior and exterior angle of a regular polygon having 30 sides.
(1) 144°, 36°
(2) 156°, 24°
(3) 164°, 16°
(4) 168°, 12°
If BC : CD = 2 : 3, AE : EC = 3 : 4 and BC : AE = 2 : 3, then find the ratio of the area of ΔECD to the area of ΔAEB.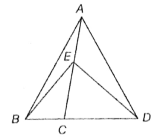
(1) 2 : 1
(2) 2 : 3
(3) 3 : 5
(4) 4 : 3
In the given figure (not to scale), O is the centre of the circle. If PB = PC, ∠PBO = 25° and ∠BOC = 130°, then find ∠ABP + ∠DCP.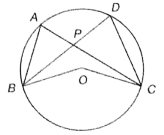
(1) 10°
(2) 30°
(3) 40°
(4) 50°
In a polygon, the greatest angle is 110° and all the angles are distinct in integral measures (in degrees) Find the maximum number of sides it can have.
(1) 4
(2) 5
(3) 6
(4) 7
In the given figure, ABCD is a rectangle inscribed in a semi-circle. If the length and the breadth of the rectangle are in the ratio 2 : 1. What is the ratio of the perimeter of the rectangle to the diameter of the semicircle?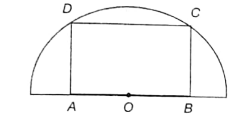
(1) 3 :
(2)
(3)
(4)
In the given figure, the diameter of the circle with area π sq. units. Another circle is drawn with C as centre, which is on the given circle and passing through A and B. Find the area of the shaded region.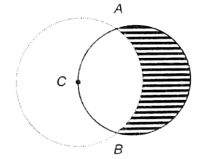
(1) sq. units
(2) sq. units
(3) 1 sq. units
(4) 1.2 sq. units
In the following figure (not to scale). C1 and C2 are two congruent circles with centres O1 and O2, respectively. Each circle passes through the centre of the other circle. If the circumference of each circle is 2 cm, the perimeter of the shaded region is _______ cm.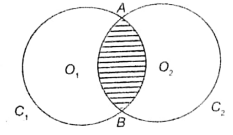
(1)
(2) 1
(3)
(4)
In the given figure (not to scale), the points M, R, N, S and Q are concyclic. Find ∠PQR + ∠OPR + ∠NMS + ∠OSN, if O is the centre of the circle.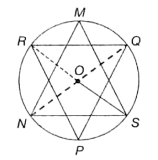
(1) 90°
(2) 180°
(3) 270°
(4) Data inadequate
In the given figure (not to scale), AC is the diameter of the circle and ∠ADB = 20°, then find ∠BPC.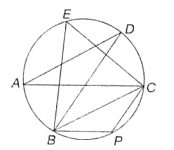
(1) 50°
(2) 70°
(3) 90°
(4) 110°
In the following figure, O is the centre of the circle and CD = DE= EF= GF. If ∠COD = 40°, then find reflex ∠COG.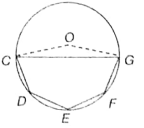
(1) 200°
(2) 90°
(3) 80°
(4) 160°
In the given figure (not to scale), AC is the median as well as altitude to BD. In ΔACE, AD is the median to CE. Which of the following is true?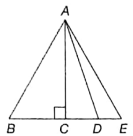
(1) AB + CD > AE
(2) AB + BC = AE
(3) AB + DE < AE
(4) None of the above
In the given figure, (not to scale), rectangle ABCD and triangle ABE are inscribed in the circle with centre O. If ∠AEB = 40°, then find ∠BOC.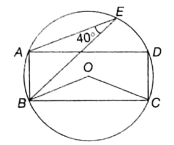
(1) 60°
(2) 80°
(3) 100°
(4) 120°
In the given figure (not to scale), O is the centre of the circle, BC and CD are equal chords. If ∠OBC = 55°, then find ∠BAC.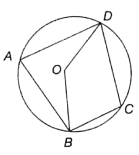
(1) 60°
(2) 70°
(3) 80°
(4) 90°
In the given figure (not to scale), O is the centre of the circle C1 and AB is the diameter of the circle C2. Quadrilateral PQRS is inscribed in the circle with centre O. Find ∠QRS.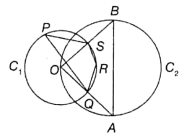
(1) 105°
(2) 115°
(3) 135°
(4) 145°
In the given figure (not to scale), E and D are the mid-points of AB and BC respectively. Also, ∠B = 90°, cm and cm. Find AC.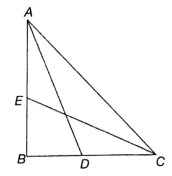
(1) 15
(2) 18
(3) 20
(4) 24
In ΔABC, P is the mid-point of BC and Q is the mid-point of AP. Find the ratio of the area of ΔABQ and the area of ΔABC. The following are the steps involved in solving the above problem.
(A) We know that a median of a triangle divides a triangle into two triangles of equal area.
(B)
(C)
(D)
(1) ACBD
(2) ADBC
(3) ABCD
(4) ADCB
ABCD is a cyclic quadrilateral, ABC is a minor arc and O is the centre of the circle. If ∠AOC = 160°, then find ∠ABC.
The following are the steps involved in solving the above problem. Arrange them in sequential order.
(A) We have, ∠ABC + ∠ADC = 180°
(B)
(C) ∠ABC = 180° – 80o
(D)
(E) ∴ ∠ABC = 100°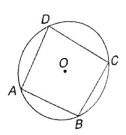
(1) ABDEC
(2) ABDCE
(3) BCDAE
(4) BACDE
Show that each diagonal of a parallelogram divide in into two congruent triangles.
The following are the steps involved in showing the above result. Arrange them in sequential order.
(A) In ΔABC and ΔCDA, AB = DC and BC = AD ( opposite angles of parallelogram) AC = AC (common side).
(B) Let ABCD be a parallelogram. Join AC.
(C) By SSS congruence property,
(D) Similarly, BD divides the triangle into two congruent triangles.
(1) BACD
(2) BDAC
(3) BADC
(4) BDCA
Show that any angle in a semi-circle is a right angle.
The following are the steps involved in showing the above result. Arrange them in sequential order.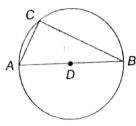
(A)
(B) The angle subtended by an are at the centre is double of the angle subtended by the same arc at any point on the remaining part of the circle.
(C) Let AB be a diameter of a circle with centre D and C be any point on the circle. Join AC and BC.
(D) ∴ ∠ADB = 2 × ∠ACB
180° = 2∠ACB (∵∠ADB = 180°)
(1) DBAC
(2) DBCA
(3) CBAD
(4) CBDA
A, B, C, and D are concyclic, AC bisects BD. If AB = 9 cm, BC = 8 cm, and CD = 6 cm, then find the measure of AD.
(1) 7 cm
(2) 10 cm
(3) 12 cm
(4) 15 cm
In the given figure, PQRS is a parallelogram, A and B are the mid points of and respectively. If PS = BR, then the quadrilateral ADBC is a _______.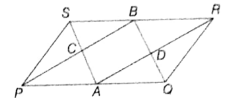
(1) rhombus
(2) trapezium
(3) square
(4) rectangle
The sides of a triangle are 2006 cm, 6002 cm and m cm, where m is a positive integer. Find the number of such possible triangles.
(1) 1
(2) 2006
(3) 3996
(4) 4011
If a, b and c are the lengths of the sides of a right triangle ABC with c = 2a and b2 – 3a2 = 0, then ∠ABC = _______.
(1) 60°
(2) 30°
(3) 45°
(4) 90°
In ∠ABC, AC = BC, S is the circum-centre and ∠ASB = 150°. Find ∠CAB.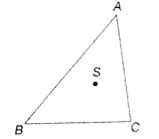
(1)
(2)
(3)
(4)
In the given figure, P, Q, R and S are concyclic points, and O is the mid-point of the diameter QS.
If ∠QPR = 25°, then find ∠SOR.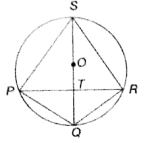
(1) 130°
(2) 120°
(3) 75°
(4) 100°
In ΔABC, ∠B = 90°. P, Q and R are the mid-points of , and respectively. Then which of the following is true?
(1) A, P, Q and R are concyclic points
(2) B, P, R and Q arc concyclic points
(3) C, Q, P and R are concyclic points
(4) All of these
If p, q and r are the lengths of the sides of a right triangle, PQR, and the hypotenuse , then ∠QPR = _______.
(1) 30°
(2) 45°
(3) 60°
(4) 30°
In a triangle PQR, PQ = QR. A and B are the mid-points of and respectively. A circle passes through P, Q, A and B. Then which of the following is necessarily true?
(1) ΔPQR is equilateral
(2) ΔPQR is right isosceles
(3) PQ is a diameter
(4) Both (1) and (3)
In the figure given below (not to scale), D is a point on the circle with centre A and C is a point on the circle with centre B. and . Then which of the following is true?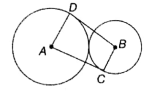
(1) BD = AC, when AD = BC
(2) BD = AC, when
(3) Both (1) and (2)
(4) BD = AC is always true
In the given figure, the angles ∠ADE and ∠ABC differ by 15°. Find ∠CAE.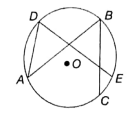
(1) 10°
(2)
(3) 15°
(4) 30°
In the given figure, ABCD is a cyclic quadrilateral, ∠ABC = 70°, bisects ∠CFA, bisects ∠DEB, ∠DCE = 60° and ∠EGF = 90°. Find ∠HEC.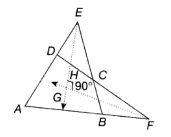
(1) 20°
(2) 40°
(3) 25°
(4) 45°
In the given figure, A, D, B, E and C are concyclic If ∠ACB = 60° and ∠AED = 50°, then find ∠DEB.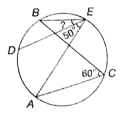
(1) 15°
(2) 10°
(3) 20°
(4) 5°